bmigrate is a graphical high-performance scientific application simulating the island model for evolutionary algorithms. This manual documents the theory, operation, and implementation of bmigrate version 0.2.2. It is a work in progress: if you notice inconsistencies or wish clarification, please contact us through the links given on the main page.
Theory
In this chapter, I'll describe the general functionality of bmigrate. When operating a bmigrate instance, you'll execute one or more simulations, which test the behaviour of a game configuration. More specifically, a simulation consists of one or more simulation runs, each consisting of a finite sequence of generations implementing [moran62]. In the simplest case, a bmigrate simulation executes the following:
- Initialise a simulation with a fixed number of islands $N$, individuals per island $n$, migration probability $m$, utility function $\pi$, and strategy domain $X$. These parameters are collectively called the simulation configuration, and are consistent within each simulation.
-
Iterate over simulation runs:
- Initialise all individuals as incumbents, each individual on an island, then assign one individual as a mutant. Assign a strategy to each individual based on the individual's type, incumbent or mutant. A strategy is a real-valued parameter $x$ passed to the utility function $\pi$. The effect is a population of individuals with a uniform incumbent strategy $x$ spread over $N$ islands and a single individual with a mutant strategy $y$.
-
Iterate over generations:
- On each island, compute each individual's number of offspring (reproduction), which inherit the parent's type. The count of offspring is determined by the individual's strategy $x_i$, all other individuals' strategies $x_{-i}$, and the utility function $\pi$. The reproduction count is based on a Poisson random number with the mean, $\lambda$, computed from the above values.
- Assign individuals' offspring to islands (migration). Probability of migration is determined by the simulation parameter $m$, though emigration is implemented in several ways, the simplest being selection of a random island.
- On each island with immigrants, replace a single inhabitant with a migrant (selection and replacement), then repeat.
- Terminate the run after a fixed number of generations or when the global mutant or incumbent tally reaches zero.
- Re-assign the incumbent strategy, mutant strategy, initial mutant's island, and repeat.
See Notation for a review of the mathematical notation and variable names.
In the remaining sections of this chapter, I closely consider each step of the above sequence.
Generations
When a generation begins, each island consists of a non-zero number of individuals of either a mutant or incumbent type, each with an assigned type-specific strategy. A generation proceeds exactly as follows:
- Compute an individual's reproductive fertility from a Poisson-distributed random number with mean $\alpha(1 + \delta\pi(x_i, x_{-i})$, where $\pi$ is a function accepting the individual's strategy $x_i$ and all other individuals' strategies $x_{-i}$ on her island. For example, on an island with two individuals having strategies $x = 5$ and $y = 2$, with the function simply being $x_i + x_{-i}$, the first individual's fertility is $\alpha(1 + 15\delta)$ and the second individual's is $\alpha(1 + 12\delta)$. Since fertility is Poissonian, it is never negative.
- Once each individual's offspring count has been computed, the offspring (which inherit the parent's type) migrate to other islands. With probability $m$, an offspring will migrate to a randomly-selected other island. Otherwise, the offspring will migrate to the parent's (i.e., the current) island.
- Lastly, on each island with a queue of individuals migrated from other islands (or the same island), a single randomly-selected individual replaces a single randomly-selected individual on the island. If an island has no waiting individuals, nothing happens to that island.
The tally of mutants and incumbents globally and per-island is recomputed following each generation.
Runs
A simulation run begins with all individuals but one being incumbents. The mutant type is assigned to a single individual in the total population. Each individual is assigned a strategy $x_i$ based on their type. A simulation run proceeds exactly as follows:
- Execute a single generation.
- Increment the generation count.
- If the generation meets a fixed termination count, stop the run. If the global tally of mutants or incumbents reaches zero, stop the run. Otherwise, repeat.
When a simulation run terminates, the fraction of mutants remaining is recorded. After accumulating statistics, the run is re-started in its initial configuration with mutant strategy, incumbent strategy, and initial mutant island re-assigned.
Simulation
Simulations are configured with a number of islands $N$, individuals per island $n$ (which may be non-uniform), migration probability $m$ (which may be non-uniform and asymmetric), utility function $\pi$, and strategy domain $X$, maximum generation $T$, and variables $\alpha$ and $\delta$ for transforming utility into the Poisson mean. A simulation repeats runs until stopped or paused by the system user.
For each run, the incumbent strategy is assigned from a discrete grid over the real-valued strategy domain $X$. The grid's boundaries are inclusive of the domain's lower bound, non-inclusive of the domain's upper bound. Thus, if $X \in [0, 1)$ and the grid has 100 slots, possible strategies will be $0, 0.01, 0.02, \cdots, 0.99$. The mutant strategy may be configured in two ways:
- After each simulation run, the mutant strategy is assigned from the next grid position, e.g., from 0.01 to 0.02. If the grid position is at the upper bound, it is re-set to the lower bound. The incumbent strategy is only re-assigned when the mutant grid position is re-set to the lower bound. This behaviour ensures that all mutants and incumbents are treated equally over many simulation runs.
- The mutant strategy is assigned from a Gaussian distribution with a preconfigured standard deviation and the mean set to the incumbent strategy. The strategy is redrawn until it falls within a strategy domain that intersects $X$, inclusive of the lower bound, non-inclusive of the upper bound. The incumbent strategy is re-assigned when the number of mutants for that incumbent have reached the number of slots.
When the incumbent strategy reaches its upper bound, it resets to the lower bound. At this point, the initial mutant island is also incremented. The initial mutant island will also wrap when it completes the last island.
Implementation
Being a high-performance scientific application, bmigrate concerns itself a great deal with mechanics such as randomness, parallelism, and data-flow. This section briefly touches upon these concepts.
Data-Flow
Data-flow defines how data moves from simulations to graphed output. Having data analysed or graphed directly from simulation data would significantly slow down data collection. To minimise simulation and interface stalling, data is copied and translated in several stages. In general, data is produced by the simulation threads and consumed, periodically and in several stages, by the main graphical thread.
- Hot Storage
- Statistics (e.g., on-line mutant fractions mean per incumbent) are written directly to hot storage by simulation threads. Hot refers to the high frequency of data access between the simulation threads.
- Hot Storage Look-aside Buffer
- When the main graphical thread wishes to read fresh data for graphical display, it sets a copy flag to copy-out. The first simulation thread to see that this flag has been set to copy-out updates the flag to copy-pending and copies the hot storage into a look-aside bufffer. Hot storage may then continue to be modified by the simulation threads.
- Warm Storage
- After copying data from hot storage into a look-aside buffer, the thread that updated the copy flag copies the look-aside buffer into warm storage. Warm refers to the low frequency of data access between the main graphical thread and the copying simulation thread. During the copy, the thread also performs more expensive statistical operations (such as minimum mutant fraction, or fitting of data) as it copies the data. The thread then clears the copy flag.
- Cold Storage
- When the main graphical thread detects that the copy flag has been cleared, it copies from warm storage into cold storage. Cold means that the data is not changed by anybody but the controlling (graphical main) thread. The main graphical thread also performs some statistical analysis during the copy.
This sequence ensures a minimum degree of contention between threads. The main graphical thread needs only to wait for the copy flag to be unset before copying the data into its own thread of operation. The simulation threads need only wait for the look-aside copy, at which point only one thread is used for remaining data copy and statistical analysis.
Parallelism
Simulations may be executed in parallel if assigned multiple threads during configuration. By default, each simulation is assigned a single thread. Thus, there are several moments when synchronisation between threads occurs to ensure simulations and data-flow processes are race-free with minimum contention.
- Before each simulation, assignment of incumbent and mutant strategies must be synchronised. The index for both of these strategies increases monotonically within a critical section (modulo the lattice dimensions). For Gaussian-distributed mutants, of course, the mutant monotonicity is irrelevant.
- After each simulation, the result for a given incumbent must be tallied in a critical section. This is required because, in some situations, a single run might take long enough that another processor starts running with the same incumbent, with both finishing simultaneously.
- When data is copied from hot storage into the look-aside buffer, it is copied within a critical section. This prevents partial modification to the data in-copy.
- When the main graphical thread requests a data copyout, it does so in a critical section. This ensures that only a single simulation thread will perform the copyout, and also that the main calling thread won't have its copyout flag unset before all data has been copied.
Randomness
By default, bmigrate uses the MT19937 (Mersenne-Twister) generator of [matsumoto98]. This ensures good-quality randomness with a very high period. (There is currently no facility in bmigrate for handlng period roll-over.)
Each simulation thread is allocated its own randomn number generator. Each generator is assigned seed from arc4random, which is implemented differently across operating systems. This ensures that all threads produce independent random variables.
Precision
All floating-point operations of bmigrate use double-precision (type double) floating point numbers. The statistical algorithms used (see links to algorithm descriptions) provide robust numerical stability.
Integral operations (counters) use unsigned 64-bit integers (type uint64_t). No checking is done for additive or multiplicative overflow as a simulation with more than $2^{64}$ runs is pretty unlikely.
Installation
In short, you'll need a UNIX machine (Mac OS X, Linux, BSD, etc.) to use bmigrate. At this time, Microsoft Windows builds are not available—please contact us if you have the knowledge (and wherewithal!) to accomplish this. If you're using Mac OS X, we strongly suggest that you use the pre-compiled application bundle. Otherwise, you'll need to download and compile from the source. In general, the more powerful your machine, the better: bmigrate takes advantage of as many processors as possible. It regularly runs on machines ranging from single core laptops to a sixty-four core workstation.
Binary Installation
Application binaries are available for Mac OS X Lion (10.7) and later. To use these, simply download the application, un-archive, and double-click to run! Note: you'll probably need to configure your system to allow downloaded binaries to run: find this option in the Security & Privacy settings of your System Preferences.
Source Installation
Download the newest sources or from those the archives. Sources have been compiled and run on Mac OS X Snow Leopard (10.6) and later, GNU/Linux (Debian), and OpenBSD.
To compile bmigrate, you'll need to install a number of dependencies. (If you're running on Mac OS X, just use the binary application: it's a real pain in the neck to configure the build system for GTK+3 applications.) Consult the documentation for your operating system on how to install these.
-
gmake: GNU Make, for the build system (the
default
makeimplementation on Mac OS X and GNU/Linux) - GTK+3: GNOME Toolkit, for the graphics
- kplot: Plotting library
- GSL: GNU Scientific Library, for mathematical functions
- libbsd: BSD libraries (only relevant for GNU/Linux systems)
These are all available as packages for modern UNIX systems.
(If you're downloading and installing any components on you're own, something is wrong!)
To compile and install the software, simply run the following.
(This will use pkg-config to locate relevant GNU tools.)
% make % sudo make install
If you're on a BSD system, you may need to invoke gmake if make defaults
to the BSD implemenation of the same utility.
By default, this will install into /usr/local. To specify an alternative root, pass the PREFIX environment variable to the install command. Assuming that $PREFIX/bin is in your PATH, you can then run the system by invoking bmigrate.
Configuration
When invoked, bmigrate will pop up a configuration screen.
The configuration screen allows you to define the parameters for a simulation—the window will stay
open for as long as any simulations are running, and allow you to start new simulations along existing
ones.
To quit bmigrate, simply press Quit
.
To start a simulation (after entering configuration data), press Simulate
.
If your parameters are faulty, you will be informed as such and a simulation will not begin until you've
corrected all of the errors.
If you want to see the effects of your parameters on reproduction (i.e., given your utility function, number of
individuals per island, strategy space, and normalisation parameters), then click Range-Find
(see
Range-finding).
This will start a process that scans the strategy-space and produces the minimum, maximum, and mean values given as the
Poisson random number mean.
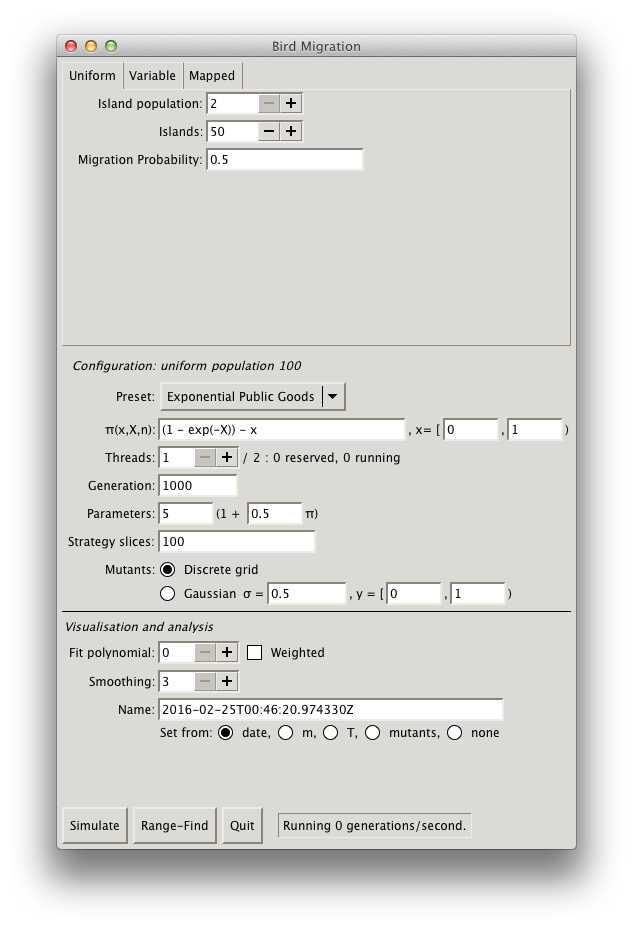
Environment Structure
Begin by assigning $N$, $n$, and $m$. This constitutes the environment structure of the game; or in other words, the physical layout of the islands, $m$ and so on. There are three distinct methods of providing this information: uniform, for uniform parameterisation across individuals and islands; variable, for non-uniform island sizes; and mapped, for non-uniform island parameterisation and inter-island configuration.
- Uniform
- The simplest (and fastest!) configuration of a fixed number of islands $N$ (at least two); a fixed, uniform number of individuals per island $n$ (at least two); and a probability $m$ of inter-island migration uniform to all [other] islands. You'll probably want to use this configuration as a baseline in simulations.
- Variable
-
Non-uniform individuals (at least two) per island.
Individual's uniform probability of migration, $m$, must also be applied.
If you specify an equal number of islanders for all islands (and zero value for the
shot-clock mean), this will revert to the uniform configuration.
You can also specify the Poisson mean of a per-island shot-clock of when an island will
be checked for
wiping out
. When an island's shot-clock elapses, the island will have its utilities summed and transformed into a probability as follows: $$ \text{coeff}\cdot\left(exp(-\sum_i \lambda_i\right) $$ Here, $\lambda_i$ is the Poisson mean of an islander $i$ given the payoff function $\pi$ and parameters. The coefficient is given in theisland death coefficient
value. If the probability is satisfied by a randomly-drawn number in the unit interval, the island is wiped out. Otherwise, the shot-clock is reset. Wiped-out islands have all of their inhabitants removed and the shot-clock, reset. For example, if an island is selected for wiping out at $t_\lambda$, and the new Poisson-random shot-clock value is $p$, the next check will be $t_\lambda + 1 + p$. At time $t_\lambda$ and after, the island will accept random immigrants until the island meets the expected population, at which point it resumes the normal random-replace method. If an island is selected to be killed off when it has no inhabitants, the shot-clock is merely reset. Obviously, islands with no inhabitants will not generate any offspring. - Mapped
-
Put individuals on islands on the Earth's surface, allowing for varying methods of
inter-island migration probability calculation.
The map type specifies how the map is supplied. It is either a KML map file populated with two or more
Placemarksections with appropriatecoordinates(see Mapping for details); a random map with a uniform number of islanders per island; or a toroidal map, where islands are evenly placed along the equator.Inter-island migration (that is, once an individual chooses to migrate with probability $m$, which island she selects) is computed as either uniform random (i.e., disregarding the game structure); the normalised inverse-square distance between each island, where distance is defined over the Earth's surface; nearest neighbour, where the nearest neighbour (over the Earth's surface) has full probability of migration; or two nearest neighbours, where the two nearest neighbours (over the Earth's surface) have even probability of migration.
The index island defines which island accepts the mutant for each simulation run. (See Runs.) In general, one will start the mutant on a random island. In some cases, however, one may fix the island. (This will be clamped to the total number of islands.)
Game-play Configuration
Next, configure the material payoff $\pi$, which dictates the reproduction of individuals. Note that payoffs are not provided directly to the Poisson generator, but are linearly transformed as described in Generations.
The utility function $\pi$ accepts the current individual's strategy $x$, the sum of all other
individuals' strategies $X$ on the individual's island, and the number of individuals $n$ on the
individual's island.
The function accepts basic binary and unary arithmetic operations, nested expressions, the
exp (exponential) function, the sqrt (square root) function, and
double-precision numbers.
You can also change the strategy domain for the incumbent's strategy, which is inclusive of the lower bound, non-inclusive of the upper bound. (The mutant's strategy domain is applied elsewhere.)
Process Configuration
Finally, configure the process machinery itself. This involves both the machinery itself and how it relates to hardware (parallelism) and also how payoffs are normalised.
- Threads
-
The number of threads of execution.
The maximum number of threads is the number of processors (or cores) of your system.
You should plan your simulations so as not to oversubscribe your machine, e.g., if you're
running 4 simulations on a 64-processor machine, you should allocate 16 threads per simulation.
(This assumes that each simulation is equally time-consuming.)
Assume that each thread will consume 100% of processor or core resources.
The number of reserved threads is the sum of all threads for simulations, regardless of state; running threads show only the count of non-paused (i.e., active) simulations.
- Generations
- The maximum number of generations per simulation run.
- Parameters
- The linear transform from utility function to Poisson process mean, $\alpha(1 + \delta\pi)$.
- Strategy slices
- This sets how finely the strategy domain is sliced for assigning incumbents and mutants (if discrete) to discrete strategies. For example, if this value is 100 (the default), then a strategy domain in the unit interval results in strategies of $0, 0.01, 0.02, \ldots, 0.99$. A higher number will make a finer mesh, but take more time to process.
- Mutants
- Determines how mutants are assigned. If discrete, mutants are assigned in slices within the strategy domain. If Gaussian, mutants are assigned from a Gaussian distribution around the incumbent strategy with the given standard deviation. The distribution is truncated to the given strategy domain, inclusive of its lower bound, non-inclusive of the upper bound. This strategy domain must be a superset of the incumbent domain $X$. The Box-Muller algorithm is used for producing Gaussian-distributed random numbers.
- Fit polynomial
- If you wish to fit incumbents' mean mutant fraction to a polynomial during run-time, you may specify the degree of that polynomial here. If set to 0, fitting will not be performed. If set to non-zero, you may also specify that the fitting be weighed by the variance of each incumbent mean mutant fraction. The fitting algorithm is the modified Golub-Reinsch SVD algorithm with column scaling.
- Name
-
A free-form name for the simulation.
Defaults to the current time.
You can set the name to auto-fill by tying it to a number of inputs.
When these inputs change, the auto-fill name will change as well.
Setting it to
None
will disable this feature.
Mapping
bmigrate has extensive support for extracting population structures from maps, specifically from and to KML map files. A common way of creating and manipulating KML files is with Google Earth.
During Configuration, one can provide a map file from which population
sizes and inter-island migration probabilities are computed.
Each island corresponds to a KML Placemark.
The coordinates of the island are extracted from its coordinates tuple.
Lastly, if the string @@population=NNN@@ appears in any text segment within the Placemark
(e.g., within the Description), the NNN will be used as the island's population.
If it isn't a valid number, it will raise an error.
The default island population is 2.
One can also save map files (as a directory of KML files, accomodating for multiple simulations). If a map was provided during configuration, the same map file is outputted, but certain key words will be replaced by the simulation statistics:
@@mean@@- The mean mutant fraction over all simulation runs when the mutant is initialised on the given island.
@@meanpct@@-
Like
@@mean@@, but normalised as a percentage of all islands' accumulated fraction. @@population@@or@@population=NNN@@- The island population.
@@stddev@@- The standard deviation of the mean mutant fraction over all simulation runs when the mutant is initialised on the given island.
Range-finding
If you click the Range-find
button, the current parameters will be used to find the
minimum, maximum, and average fecundity (Poisson mean).
The range-finder will iterate over all possible strategies for the incumbent and mutant, with
the given number of slices
over the strategy space.
Unlike in the real simulation, where mutant strategies may be randomly distributed, the
range-finder will iterate over all possible strategies over a lattice.
Thus, the average is an average over the lattice, and may not reflect the average of your
simulation!
For each configuration, all possible mutant values (up to the number of islanders) is tried.
You can stop the range-finder at any time.
Visualisation
When you've configured a simulation, press Simulate
to start the visualisation.
If all values validate, a window will pop up visualising the simulation in a variety of ways.
If values don't validate, they'll be noted and you can fix them.
Each field must be properly filled in before the simulation begins.
Don't worry—you'll be able to review your simulation's configuration while it's running!
Simulations are reference-counted: when you start a simulation, it has a single referring window. Each window visualises at least one simulation: to compare different simulations, you can drag and drop simulation windows into each other. This will increase the reference to individual simulations. The same happens if you clone a view. When you close a window, each simulation is dereferenced. When no windows reference a simulation, it will terminate.
Control
Simulation and analyses are controlled from the menu bar.
Simulations are controlled with the Tools
and File
menu.
Analysis is controlled with the View
menu.
If you're running on Mac OS X, the menu bar is the top-most menubar.
On other UNIX systems, menu bars are part of each simulation window.
File
You can perform the usual Quit
and Close
operations (the latter will
dereference each simulation, just like closing the window by way of your window
manager).
You can also Clone
your view, which will duplicate the window (including all
simulations).
You can also save a windows's current view of its simulations as a data file (described in each Views).
You can choose either PDF, PS, EPS, or PNG as possible output types.
You can export all views of all simulations into a folder as well, which will include a
README.txt of the configuration.
View
Switch the current view, which consists of one or more simulations, to another. These are listed in Views.
Tools
From here you can pause or unpause simulations. These apply to all simulations in the current window. You can also register a directory into which all views will be auto-exported once per minute. (This is handy when running extensive simulations over an iffy network.)
Views
Each window may have an arbitrary number of simulations and is connected to a particular view of those
simulations.
This is shown in the View
notebook panel of the simulation window.
The Configuration
panel lists the simulation's configuration.
You can choose a new view from the View
menu.
The current view is reflected in the window's title bar.
Mutant Mean
The sample mean graphs incumbent strategies on the $x$-axis and the mean mutant fraction after $T$ generations (or when one of the types goes extinct—whichever comes first) over all runs to date on the $y$-axis. If an incumbent does not have any runs yet, it will display as zero. The graph $y$-maximum will automatically adjust to the highest simulation peak.
Mutant Mean and Standard Deviation
This graph augments the Mutant Mean graph with the standard deviation above and below each incumbent's mean. The standard deviation below is truncated to zero when negative. The mutant mean graph is shown in a solid colour; the standard deviation above and below, in a transparent rendering of the same.
The standard deviation is computed from the unbiased sample variance algorithm of [knuth98] and [welford62]. It shouldn't be confused with the population standard deviation, which is computed over all $t$ samples (simulation runs). This is an unbiased estimate computed over $t-1$ samples.
Fitted Polynomial
If a non-zero degree for polynomial fitting was selected at Configuration, this will show the Mutant Mean (transparent line) along with the fitted polynomial (solid line). If a zero degree was selected, it will only show the Mutant Mean. If the weighted option was selected during Configuration, the standard deviation (see Mutant Mean and Standard Deviation) will be used as a weight.
Unlike the Mutant Mean or Mutant Mean and Standard Deviation,
the polynomial for this graph is computed roughly four times per second instead of with every
run.
This prevents excessive slow-down.
The implementations are gsl_multifit_wlinear and
gsl_multifit_linear for the weighted and non-weighted fitting algorithm,
respectively, of the GNU Scientific Library.
Both are described in the Statistics
chapter of [barnett96].
Mutant Extinctions
The percentage of simulation runs to date of each incumbent where the mutant population goes extinct before the maximum simulation time $T$. The $x$-axis shows incumbent strategy. The $y$-axis shows the fraction of mutant extinctions in the unit interval. If the incumbent does not yet have any data (i.e., no runs yet), it shows zero. See Incumbent Extinctions.
Incumbent Extinctions
The percentage of simulation runs to date of each incumbent where the incumbent population goes extinct before the maximum simulation time $T$. The $x$-axis shows incumbent strategy. The $y$-axis shows the fraction of incumbent extinctions in the unit interval. If the incumbent does not yet have any data (i.e., no runs yet), it shows zero. See Mutant Extinctions.
Smoothed Mutant Mean
This is the same as Mutant Mean except with the data points (sample mean per incumbent strategy on the $x$-axis) smoothed by a moving average. The degree of this moving average is set during Configuration, defaulting to three.
The moving average is computed for each interior point by replacing the current point with the average of the prior and subsequent points. The border points (i.e., the points that cannot exercise a full smooth sample) are not adjusted. The moving average is not cascading: when replacing points, the prior and subsequent point used for averaging are from the original data set, not the smoothed data set.
Smoothed Mutant Extinctions
This is the same as Mutant Extinctions except with the data points (extinction fraction per incumbent strategy on the $x$-axis) smoothed by a moving average. See Smoothed Mutant Mean for the moving average calculation.
Smoothed Incumbent Extinctions
This is the same as Incumbent Extinctions except with the data points (extinction fraction per incumbent strategy on the $x$-axis) smoothed by a moving average. See Smoothed Mutant Mean for the moving average calculation.
Fitted Polynomial Minimum (PDF, CDF)
Accumulate the minimum value of Fitted Polynomial into a probability mass function, displayed either as a PDF or as an empirical CDF.
The minimum value is the first minimum: if multiple subsequent minima are detected (a basin), they are ignored. This might skew values toward smaller minima. Minima are accumulated whenever the polynomial is re-computed. (Four times per second.)
Mutant Mean Minimum (PDF, CDF)
Accumulate the minimum value of Mutant Mean into a probability mass function, displayed either as a PDF or as an empirical CDF. See Fitted Polynomial Minimum (PDF, CDF) for details on computing the distribution.
Mutant Extinctions Minimum (PDF, CDF)
Accumulate the minimum value of Mutant Extinctions into a probability mass function, displayed either as a PDF or as an empirical CDF. See Fitted Polynomial Minimum (PDF, CDF) for details on computing the distribution.
Incumbent Extinctions Minimum (PDF, CDF)
Accumulate the minimum value of Incumbent Extinctions into a probability mass function, displayed either as a PDF or as an empirical CDF. See Fitted Polynomial Minimum (PDF, CDF) for details on computing the distribution.
Exit Times (PDF, CDF)
Accumulate the exit time of simulation runs (i.e., the time $t$ at which point the simulation exited due to extinction or reaching $T$) into a probability mass function or an empirical CDF. See Fitted Polynomial Minimum (PDF, CDF) for details on computing the distribution.
Fitted Polynomial Minimum History
Accumulate the last 256 instantaneous minimum values (approximately the last minute) of Fitted Polynomial.
Mutant Mean Minimum History
Accumulate the last 256 instantaneous minimum values (approximately the last minute) of Mutant Mean Minimum.
Fitted Polynomial Minimum Mean
Plot the incumbent strategy distribution mean of Fitted Polynomial Minimum (PDF, CDF) within the standard deviation error bars (above and below), which are truncated below at zero. Each simulation is plotted as a separate point.
Mutant Mean Minimum Mean
Plot the incumbent strategy distribution mean of Mutant Mean Minimum (PDF, CDF) within the standard deviation error bars (above and below), which are truncated below at zero. Each simulation is plotted as a separate point.
Mutant Extinctions Minimum Mean
Plot the incumbent strategy distribution mean of Mutant Extinctions Minimum (PDF, CDF) within the standard deviation error bars (above and below), which are truncated below at zero. Each simulation is plotted as a separate point.
Incumbent Extinctions Minimum Mean
Plot the incumbent strategy distribution mean of Incumbent Extinctions Minimum (PDF, CDF) within the standard deviation error bars (above and below), which are truncated below at zero. Each simulation is plotted as a separate point.
Island Index Case Mutant Mean
For each island where the mutant is assigned at the simulation run start, print the mean mutant fraction after $T$ generations (or when one of the types goes extinct—whichever comes first) over all runs to date. In other words, accumulate, given an island, how robustly a starting mutant behaves.
Island Mutant Mean
Accumulate the mutant mean (as in Mutant Mean) of each island.
Notation
The following notation is used consistently throughout this document and the system itself.
- $\alpha$
- The outer multiplier for the linear transform of the utility function, $\alpha(1 + \delta\pi(x_i, x_{-i})$.
- $\delta$
- The inner multiplier for the linear transform of the utility function, $\alpha(1 + \delta\pi(x_i, x_{-i})$.
- $\lambda$
- The mean of a Poisson distribution. Poisson means are used for reproduction and, if so configured, the island death shot-clock.
- $m$
- For each offspring, the probability of migration.
- $n$, $n_i$
- The number of individuals per island $n \geq 2$. If the islands have a uniform population size, then this number is constant; otherwise, it may be non-uniform $n_i$ where $i$ is the fixed index of an island.
- $N$
- The total number of islands $N \geq 2$.
- $\pi$
- The payoff function. This accepts three variables: $x$, the strategy of the current individual; $X$, the sum of all individuals' strategies; and $n$ , the number of individuals.
- $T$
- The maximum number of generations $T > 0$ for which a simulation run will run.
- $X$, $x$, $x_i$, $x_{-i}$
- The real-valued strategy domain, a single strategy in that domain, an individual $i$'s strategy, and all other individuals' strategies.
Bibliography
- R. M. Barnett (1996). The Review of Particle Physics, D.54. Particle Data Group (PDG).
- Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edition, p. 232. Boston: Addison-Wesley.
-
Makato Matsumoto and Takuji Nishimura (1998).
Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudorandom Number Generator
. ACM Transactions on Modeling and Computer Simulation 8(1): 3–30. - Patrick Alfred Pierce Moran (1962). The Statistical Processes of Evolutionary Theory. Oxford: Clarendon Press.
-
B. P. Welford (1962).
Note on a method for calculating corrected sums of squares and products
. Technometrics 4(3): 419–420;